最近,我校数理学院师资博士后赵伟峰在格子Boltzmann方法的边界处理方面取得新进展,相关结果以“Boundary Conditions for Kinetic Theory Based Models I: Lattice Boltzmann Models”为题在应用数学顶级期刊SIAM系列杂志《Multiscale Modeling and Simulation》上发表。
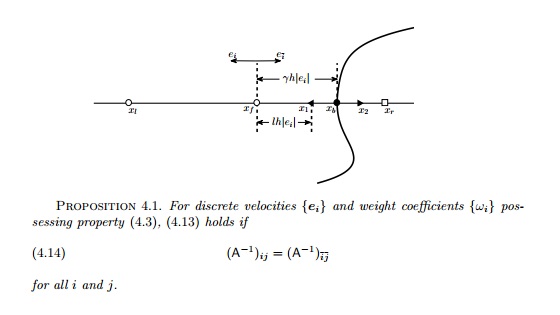
格子Boltzmann方法是一种基于动理学理论的数值方法,广泛应用于复杂流动的数值模拟,其边界处理是一个关键问题。赵伟峰博士及其合作者对该方法提出了一类有效的边界处理格式,这类格式只依赖于当前计算格点,具有良好的数值稳定性,并且对曲边界具有二阶精度。该论文还对格子Boltzmann方法半反弹格式的二阶精度提出了一个简洁的充分条件,并证明了常用的多松弛模型满足该条件,从而澄清了半反弹格式的精度问题。

赵伟峰博士于2013年本科毕业于华中科技大学,2017年博士毕业于北京计算科学研究中心,随后入职北京科技大学数理学院。最近一年,赵伟峰博士以第一作者或通讯作者身份发表3篇论文。主持国家自然科学基金青年基金项目1项、中国博士后科学基金面上项目1项、中央高校基本科研业务费项目1项。